从自编码器视角重新发明VAE,Diffusion和Flow Matching
本文所涉及的算法重新发明过程,纯属本人虚构,如有雷同,纯属巧合。
前言:历史的起点
2006年,Hinton在《Science》上发表了一篇具有里程碑意义的文章:“使用神经网络降低数据维度”(Reducing the Dimensionality of Data with Neural Networks)。他使用了一种叫做自编码器(Autoencoder / AE)的神经网络,将高维输入投影到低维空间,再从低维空间中重构原始数据。这个自编码器(AE)取得了比主成分分析(PCA)和核主成分分析(Kernel PCA)都更好的重建效果。
在那个年代,深度神经网络的训练方法还不够成熟。Hinton需要提出一种精巧的逐层预训练算法——受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)——来初始化一个9层的多层感知机。两年后,Pascal Vincent等提出了堆叠降噪自编码器(Stacked Denoising Autoencoders),证明它在无监督网络初始化方面的性能优于RBM。再往后,人们发现随机初始化已经足够好,这些预训练技术变得不再必要。
在这篇博客中,我将带大家穿越时空,回到历史的原点,看看自编码器是如何一步步引向今天生机勃勃的生成式AI时代。这篇文章将基于原始直觉和合理的想象,来复现变分自编码器(VAE)、扩散模型(Diffusion)、流匹配(Flow Matching)等技术的发明过程。你会发现,自编码器提供了一个独特的观察世界的视角,将几个看似独立的模型串联起来,整个技术演进的脉络变得清晰而连贯。
本文所有实验都在MNIST数据集上完成。我曾经忽视这个玩具数据集,因为除了手写数字识别外,它的实际应用非常有限。但现在我意识到,在发明新东西时,保持实验设置尽可能简单和切题是非常重要的。灰度图像、小分辨率——这些是图像最简单的形式,但仍然包含了一切的本质。
现在假设你是生活在2006年的一个研究员。你刚看到了Hinton的论文,打算自己动手实现一下。我们假设你能利用现代的工具:Pytorch, AdamW optimizer,现代GPU等等,但是你的思路局限在2006年大家的对于世界的认知。
第一步:复现Science论文中的自编码器 code
Science论文中的自编码器其实非常简单。它有九层,神经元数量分别为:784-1000-500-250-30-250-500-1000-784。第一层和最后一层都有784个神经元,因为MNIST图像大小为28×28=784像素。你使用Sigmoid函数作为非线性激活层,使用均方误差损失作为训练信号。
经过100个epoch的训练,你的模型在测试集上取得了相当理想的表现,损失约为3.36。作为对比,Hinton在论文中报告的结果是3.00,而这两个数字都远远优于kernel PCA的8.01。从重建效果来看,生成的图像已经与原始图像几乎无法区分,因此你认为没有必要继续打磨这个测试误差——虽然进一步优化并非难事,但过程会较为繁琐,投入产出比不高。
值得注意的是,原始图像的维度从784维压缩到了仅仅30维。这30维的隐变量(我们记作$z$)就像生物的DNA一样,浓缩编码了图像的几乎全部关键信息。
原始图像(左)和重建图像(右)如下所示:

第二步:思考——能否生成全新的图像?
此时,你凝视着右侧的重建图像,陷入了深思。确实,我已经掌握了一种生成图像的方法——这本身就是巨大的进步!但这个方法存在一个明显的局限:它只能复制输入,生成与原图一模一样的输出。如果能够创造出全新的图像——一张训练集和测试集中从未出现过的照片——那将是质的飞跃。这种创造能力意味着我们对图像本质有了更深刻的理解,正如那句名言所说:造不出来,就算不上真正懂它(If I can’t make it, I don’t understand it)。
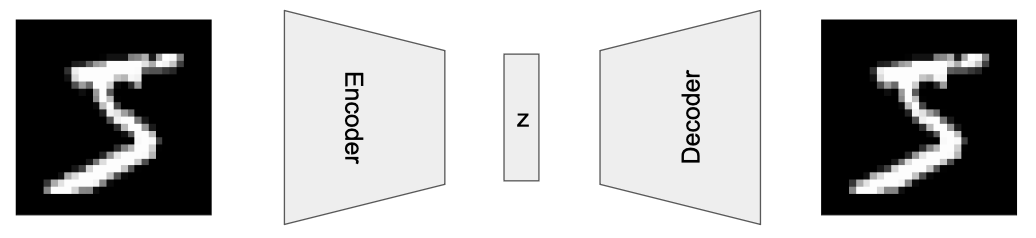
你久久凝视着这个编码器-解码器架构。前半部分并不陌生——在分类任务中经常使用这样的结构,这正是判别式AI(Discriminative AI)的典型范式。真正神奇的是后半部分:解码器能够将一个仅有30维的隐向量$z$,重新展开、还原到完整的图像空间。这才是关键所在。
第三步:探索嵌入空间 code
你蠢蠢欲动:如果把这30维向量稍微做点改动,会发生什么?如果给它加一个小小的噪声呢?例如,0.1倍的正态分布噪声。你发现,生成的图像还是跟输入一模一样。

那如果把最后几维抹掉呢?生成的图像和输入仍然高度类似原始图像。

这并不奇怪,因为图像特征空间在局部是连续的。
只是为了好玩,你用一个随机噪声作为输入,结果发现输出的图像已经很难辨认。

第四步:引入高斯混合模型 code
这时候,你陷入了更深的思考。我们应该对图像特征空间有一个基本的假设,即建立它的一个概率分布模型,并通过已有的样本来拟合这个模型。这时候你脑海里闪过几个字:高斯混合模型(Gaussian Mixture Model)。在物理里面有句话:遇事不决,量子力学;而它的概率论版本就是:遇事不决,高斯混合。(搞笑) 我们假设图像特征遵循高斯混合模型。通过简单的工具(比如sklearn里面的GaussianMixture),我们将训练数据通过编码器生成的隐向量$z$进行拟合,然后从拟合到的模型采样,输入到解码器中——瞧!

这时候,你内心心潮澎湃——这个理论是有效的!我生成了世界上从未出现过的新图片!你为这个重大发现感到欣喜。盯着这几个并不完美的数字,你对未来充满了信心。
第五步:走向变分自编码器(VAE)code
在你过度兴奋之前,你的头脑冷静了下来。这个方法存在一个明显的短板:它不支持在线学习(online learning),必须依赖一个离线步骤——高斯混合模型的拟合过程。你不禁思考:能否实现端到端的学习,直接建立从已知分布到图像分布的映射?
一个想法浮现:如果在自编码器的框架下,对30维的隐特征施加约束,让它既能准确重建原图,又服从某个已知的分布,那么训练完成后,只需从同一分布中采样,就能源源不断地生成新图像。问题的关键在于:如何让隐特征服从特定分布? 不妨从最简单的高斯分布入手。
你意识到,这是个棘手的挑战,需要突破传统思维框架。你需要放下一些固有观念,用概率论的视角重新审视这个世界。核心的转变是:这个隐变量$z$(embedding)本质上是随机变量,而非确定值 。我们其实并不确定$z$该是什么样——甚至连维度都不确定。30维可以重建图像,40维不也可以吗?答案显然是肯定的。即便固定在30维,我们已经观察到,$z$的微小扰动并不影响重建质量。因此,$z$不是一个点,而是一个概率分布,就像量子力学中的电子云,是一团概率的迷雾。
传统自编码器会沿着最小化重建误差的方向优化$z$,而现在的目标是:让$z$从高斯分布中采样时,都能成功还原原图。你设想:每次前向传播时,从高斯分布中采样一个$z$值,再送入解码器计算重建误差。但随即遇到新问题——当$z$由随机采样决定而非编码器输出时,反向传播链条被切断了:我们无法对随机数生成器求导,编码器也就无法获得梯度更新。
辗转反侧,你终于在深夜迎来顿悟——重参数化技巧(Reparameterization Trick):高斯随机变量可以表示为标准正态分布变量$\epsilon \sim \mathcal{N}(0,1)$的函数,即 $z=\mu + \sigma \times \epsilon$,其中$\mu$和$\sigma$分别是均值和标准差。前向过程中,编码器输出$\mu$和$\sigma$,同时从$\epsilon$采样一个数据点,生成$z$传入解码器。后向过程中,重建误差梯度顺着$\mu$和$\sigma$传回到编码器。
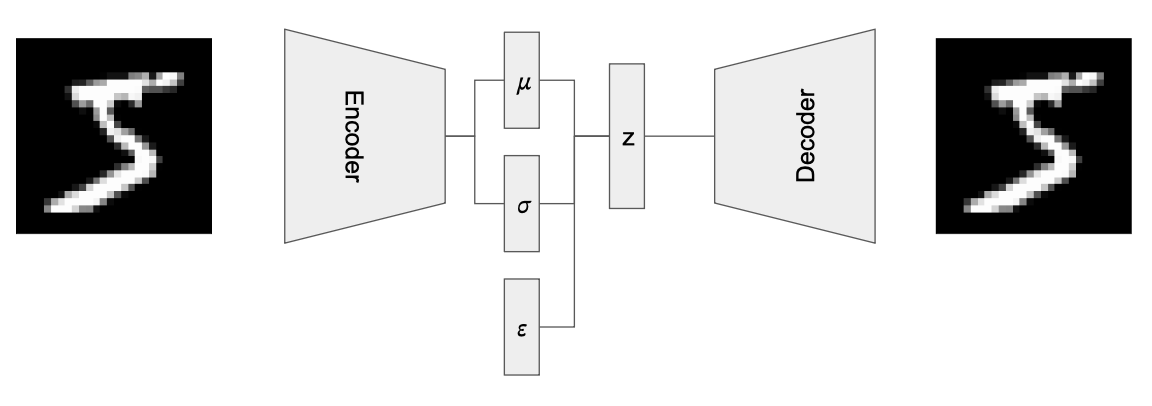
但这还不够。你需要约束$z$接近标准正态分布。如何衡量两个概率分布的相似度? KL散度(KL Divergence)是这个问题的黄金答案。经过推导,你需要在损失函数中加入:
$$\frac{1}{2}(\mu^2 + \sigma^2 - \log(\sigma^2) - 1)$$
这是一个多目标优化问题——既要最小化重建误差,又要最小化$z$与标准正态分布的KL散度。你仔细调节两个目标的权重,确保它们产生的梯度相互平衡,不被彼此淹没。
模型训练完成后,你从标准正态分布中采样,将样本送入解码器:

全新的图像诞生了——这些数据由端到端的在线学习算法生成,简洁而优雅。你感到深深的满足,那是一种难以言表的成就感!
第六步:质疑与反思
你开心了好久,把这个方法分享给你的同事。你非常满意自己的工作,打算就此收手。但过了一段时间,你的同事告诉你:你这个方法生成的图像比较模糊。另外也有人提出质疑:用来平衡两个误差的权重是一个很难优化的超参数……
第七步:走向扩散模型 code
你又陷入了长期的思考。
回归第一性原理,你开始质疑:我们的初衷不就是想从一个概率分布推断另一个概率分布吗?为什么非要纠结于信息压缩这个维度(也就是那个$z$向量)?为什么不能直接从随机噪声生成图像?对啊,为什么不行呢?
你立刻动手做了个简单实验:让自编码器直接从输入的随机噪声预测图片,用预测图像与真实图像之间的MSE作为损失函数。结果发现网络输出极其模糊:

这个网络似乎只学会了数字的"平均长相"。你意识到,想让网络从完全随机的噪声一步到位生成清晰图像,难度实在太大了。
就在这时,灵光乍现!你想起了之前接触过的降噪自编码器(Denoising Autoencoder):一个自编码器可以轻松地从轻微受损的图像重建出原图,那这个思路能不能推而广之?你在纸上涂涂画画,最终勾勒出这样一个流程:
原始图像 → 轻度污染 → 中度污染 → 重度污染 → 完全噪声
既然网络能从轻度噪声恢复原图,那能不能从中度噪声恢复到轻度噪声?更进一步,能不能从完全噪声恢复到重度噪声?思路豁然开朗——关键是要为网络设计一条渐进的学习路径!如果从噪声到图像的跨度太大,那就把它拆解成多个小步骤,网络学起来应该就容易多了。
接下来的问题是:如何设计这条学习路径?如何给图像逐步添加噪声?你清楚地意识到,这需要一些数学工具的支持。 准备好迎接一些符号和公式了吗?别担心,我保证只用最必要的那些。
我们假设$x_0$是原始图像,${x_t (0 \le t \le T,t \in \mathbb{Z})}$作为第$t$次加噪声后的图像。假设每次添加的都是高斯噪声$\mathcal{N}(0, \beta_t)$,其中$0 \lt \beta \lt 1$用于控制噪声强度。为了确保连续加噪后图像方差保持稳定,需要将原图缩放至$\sqrt{1-\beta_t}$倍。已知$x_{t-1}$的条件下,$x_{t}$的分布可以表示为:
\[q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t I) \tag{1}\]
为了简化推导,令${\alpha_t = 1-\beta_t}$和$\bar{\alpha}_t = \prod^{t}_{0} \alpha_t$。用$\epsilon, \epsilon_{t-1}, \epsilon_{t-2}, \tilde{\epsilon}_{t-2}$表示标准正态分布的随机变量。公式(1)可以改写成如下形式:
$$ \begin{aligned} x_t & = \sqrt{{\alpha}_t} x_{t-1} + \sqrt{1-{\alpha}_t} \epsilon_{t-1} \\ & = \sqrt{{\alpha}_t}(\sqrt{{\alpha}_{t-1}}x_{t-2} + \sqrt{1-{\alpha}_{t-1}}\epsilon_{t-2}) + \sqrt{1-{\alpha}_t}\epsilon_{t-1} & \text{\small 展开} x_{t-1}\\ & = \sqrt{{\alpha}_t {\alpha}_{t-1}}x_{t-2} + \sqrt{{\alpha}_t(1-{\alpha}_{t-1})}\epsilon_{t-2} + \sqrt{1-{\alpha}_t}\epsilon_{t-1} & \text{ \small } \\ & = \sqrt{{\alpha}_t {\alpha}_{t-1}}x_{t-2} + \sqrt{1-{\alpha}_t{\alpha}_{t-1}}\tilde{\epsilon}_{t-2} & \text{\small 注意随机变量求和* } \\ & = … \\ & = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon \tag{2} \end{aligned} $$
(*)这里涉及两个随机变量相加,不能简单套用结合律。两个独立高斯分布叠加后仍是高斯分布,新分布的均值为原均值之和,方差为原方差之和。因此新方差为:${\bar{\alpha}_t(1-\bar{\alpha}_{t-1}) + {1-\bar{\alpha}_t = 1-\bar{\alpha}_t\bar{\alpha}_{t-1}}}$。
公式(2)给出了从$x_0$直接得到$x_t$的快捷方式。同样的,对于$x_{t-1}$有:
\[ x_{t-1} = \sqrt{{\bar{\alpha}_ {t-1}}} x_0 + \sqrt{1 - \bar{\alpha}_{t-1}} \epsilon \tag{3}\]
至此,前向过程(给图像加噪)已经明确。接下来是核心挑战——后向过程:从噪声恢复图像。你需要计算在已知$x_t$条件下$x_{t-1}$的分布。你盯着公式(2)和(3)反复琢磨,发现它们有两个共同的变量$x_0$和$\epsilon$,联立求解并消去其中一个,公式会大大简化。
两种消元方式在数学上等价,这里以消去$x_0$为例。从公式(2)得到:
$$x_0 = \frac{1}{\bar{\alpha}_t} (x_t - \sqrt{1-\bar{\alpha}_t}\epsilon)$$
代入公式(3)并整理:
$$x_{t-1} = \frac{\bar{\alpha}_{t-1}}{\bar{\alpha}_t}(x_t - \sqrt{1-\bar{\alpha}_t}\epsilon) + \sqrt{1-\bar{\alpha} _{t-1}}\epsilon \tag{4}$$
现在$x_{t-1}$被表示成了$x_t$和$\epsilon$的函数,如果能知道随机变量$\epsilon$的具体取值,一切将迎刃而解。最后一块拼图被你找到,用参数为$\theta$的神经网络来学习$\epsilon$!即优化损失函数:${\Vert \epsilon - \epsilon_{\theta}(x_t, t) \Vert_2}$。
一切变得很清楚,训练时,网络从$x_t$和$t$预测$\epsilon_\theta$;采样时,将$x_t$和$\epsilon_\theta$代入公式(4),从$t = T, T-1, …, 1$逐步迭代,直至得到最终图像$x_0$。
你兴奋地将其写入代码。观察训练过程,发现损失虽在下降但很难降到很低,生成的图像也很模糊。你意识到可能哪里出了问题,但不能慌,不能轻易否定这个思路。仔细检查代码后,你发现MLP可能已经力不从心,需要更强大的、专为图像设计的网络结构。从"图生图"的应用场景出发,你想到可以从图像分割等任务中汲取灵感。搜索记忆后,UNet浮现在脑海——一个类似自编码器(先降维再升维)的全卷积架构。
你将模型替换为UNet,重新运行代码。图像生成的瞬间,你屏住呼吸。当屏幕上出现清晰的数字图像时,你知道成功了。你给这个模型命名为"扩散模型":就像墨水滴入清水般,你将噪声扩散进图像,再借助神经网络预测噪声并成功恢复原图。

第八步:流匹配——更直接的路径 code
你凝视着这些图像,意识到自己创造了一个非常了不起的东西——一个严谨的数学框架。但大脑深处始终有个声音挥之不去,告诉你这里面还缺了些什么,具体是什么,你一时说不清。
渐渐地,那个声音越来越清晰:直觉缺失了。没错,你一向依赖的直觉迷失在繁复的数学公式中了。你再次回到第一性原理,思考哪里还能简化。既然目标是设计一条从噪声到图像的路径,那除了给图像逐步加噪这种方法,还有没有更简单、更本质的方案?
你脑海中浮现出一条直线,从噪声笔直通向图像——线性插值。为什么不走这条最近的路?
$$ x_t = t x_1 + (1-t) x_0 $$
你立刻开始实验。每轮随机生成一个$t$(0到1之间),输入$x_t$,让网络预测$x_0 - x_1$(即速度场)。此时你已经放下了从Autoencoder带来的输出必须是$x_{t-1}$的执念——如果输出前进方向更稳定,为什么不这样做?采样的时候,从$x_1$(纯噪声)出发,每次预测$x_0 - x_1$,但只走一小步,然后以这个新的图像重新预测$x_0 - x_1$,直到走完所有步数到达$x_0$(真实图像)。
你把扩散实验的代码改了几行,开始训练。网络的loss持续下降,好兆头!你可视化了采样的输出–成功了!这种简单直接的路径同样有效!不知不觉间,你发明了流匹配算法。
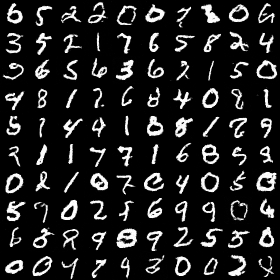
结语:直觉的力量
从自编码器到VAE,从扩散模型到流匹配,这一路走来,你没有淹没在复杂的数学推导中,而是从简单而深刻的直觉出发。每一次创新都源于对问题本质的追问:你真正想要的是什么?有没有更简单、更直接的方法?
这就是我想传递的学习范式:不要被数学公式吓倒,而是要建立直觉,理解问题的本质,然后用最简单的方式去解决它。正如爱因斯坦所说:“如果你不能简单地解释它,说明你还没有真正理解它。”
生成式AI的时代已经开始,而它的起点,就在那个朴素的自编码器里。